Comprendre et Utiliser les Quartiles, UCL/LCL et UNPL/LNPL pour Optimiser vos Processus

Dans le cadre de la gestion des processus, la surveillance des performances est essentielle pour assurer la stabilité et l’efficacité.

Pour ce faire, différentes méthodes statistiques existent afin d’analyser les variations dans les flux de travail et d’identifier les écarts significatifs.

Parmi les outils les plus couramment utilisés, on retrouve les quartiles, les limites de contrôle (UCL/LCL) et les limites naturelles du processus (UNPL/LNPL).

Mais que signifient ces termes barbares ?

Cet article a pour objectif de démystifier ces concepts et de vous expliquer comment et quand les utiliser pour optimiser vos processus.

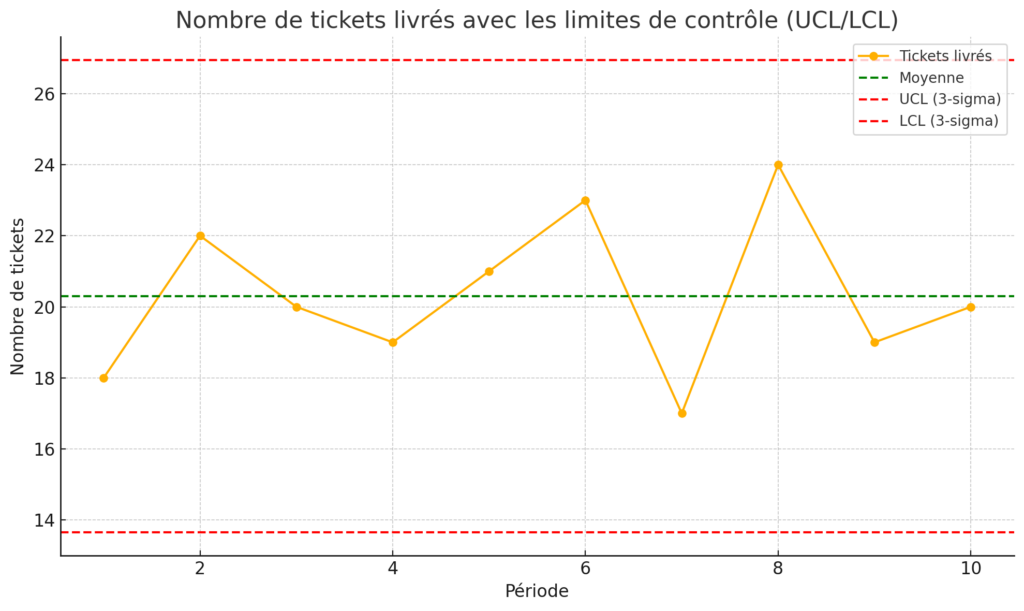
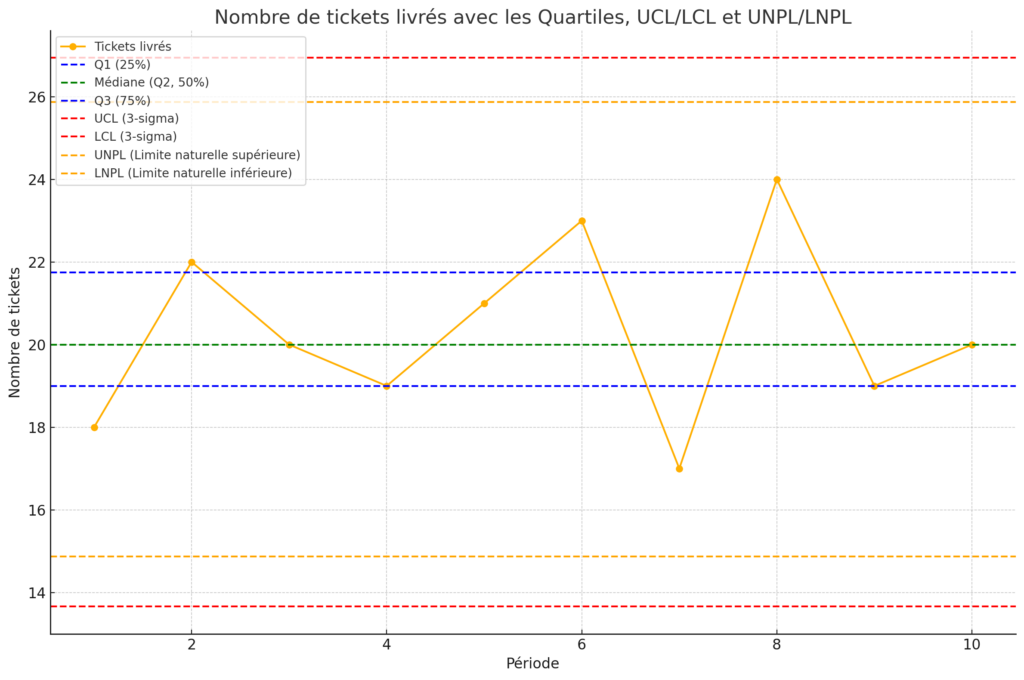
Mais avant d’entrer dans les détails de chaque concept, il serait pertinent de démarrer l’article avec un graphique illustratif qui montre le nombre de tickets livrés au fil des périodes (comme dans l’exemple que nous avons utilisé). Cela servira de base aux explications à venir.

Données d’exemple : Nombre de tickets livrés par une équipe sur 10 périodes de deux semaines : 18 ; 22 ; 20 ; 19 ; 21 ; 23 ; 17 ; 24 ; 19 ; 20

Les Quartiles : Analyser la Répartition de la performance de votre Flux (Flow Time)

Les quartiles – aussi nommées boite à Moustaches – divisent les données en quatre parties égales, permettant de comprendre comment elles sont réparties.

Ils sont particulièrement utiles pour obtenir une vue d’ensemble de la distribution des performances dans un processus.

Définition des Quartiles

  • Q1 (Premier quartile) : 25 % des données sont inférieures à cette valeur.
  • Q2 (Médiane ou second quartile) : 50 % des données sont inférieures à cette valeur.
  • Q3 (Troisième quartile) : 75 % des données sont inférieures à cette valeur.

Les écarts inter-quartiles (IQR) peuvent aussi être utilisés pour détecter des valeurs aberrantes (outliers).

L’IQR va représenter les limites basses et hautes admissible pour avoir une répartition du flux prédictible. Il s’agit des fameuses moustaches. Les valeurs se trouvant en dehors doivent être considérer comme des valeurs aberrantes et être analysées.

L’IQR est défini comme Q3−Q1.  

Une règle commune est de considérer toute valeur en dehors de Q1 − 1,5 × IQR et Q3 + 1,5 × IQR comme une valeur aberrante.

Exemple de calcul de Quartiles

  1. Trier les données par ordre croissant : 17 ; 18 ; 19 ; 19 ; 20 ; 20 ; 21 ; 22 ; 23 ; 24
  2. Calculer le Premiers Quartile – Q1 en identifiant le temps de Cycle de 25% des mesures – Résultat : Q1 = 19
  3. Calculer la Second Quartile, c’est çà dire la Médiane, représentant 50% des temps de cycle mesurés – Résultat Q2 = 20
    • Liste Impair : Lorsque le nombre de mesure est impair, prendre la valeur du milieu
    • Liste Pair : Lorsque le nombre de mesure est pair, comme dans notre exemple, Faire la somme des 2 valeurs centrale et les diviser par 2. Le résultat représente la Médiane.
  4. Calculer le Troisième Quartile – Q3, représentant les 75% des mesures effectuées – Résultat : Q3 = 22
  5. Identifier les Moustaches, c’est à dire la valeur la plus faible et la valeur la plus importante mesurée – Résultat :
  6. Calculer l’inter-quartile (IQR)
    • IQR = Q3 – Q1 = 22 – 19 = 3
    • Limite basse = Q1 – 1.5*IQR = 19 + 1,5*3 = 14.5
    • Limite haute = Q3 + 1.5*IQR = 22 + 1*5*3 = 26.5

Utilité

Les Quartiles sont souvent utilisés pour visualiser la répartition des données et identifier les points où se situent la majorité des valeurs. Cela permet de voir où se trouvent les valeurs centrales (grâce à la médiane) et d’identifier les écarts ou les valeurs aberrantes.

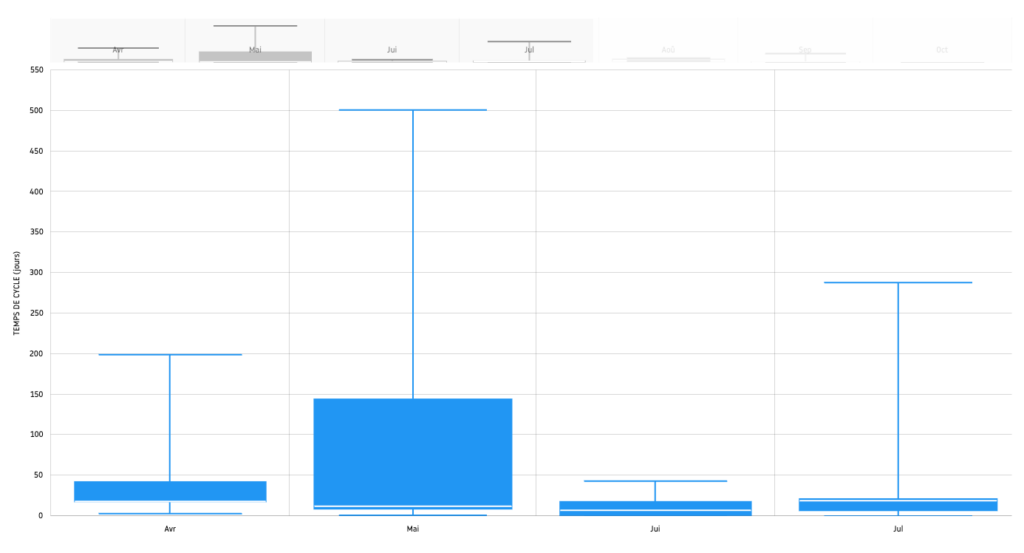
Prenons l’exemple d’une équipe de développement qui livre des tickets toutes les deux semaines. En analysant le nombre de tickets livrés sur plusieurs périodes, les quartiles nous donnent un aperçu de la répartition des livraisons. Cela aide à comprendre combien de tickets sont livrés dans les 25 % les plus bas, les 50 % centraux, et les 25 % les plus hauts.

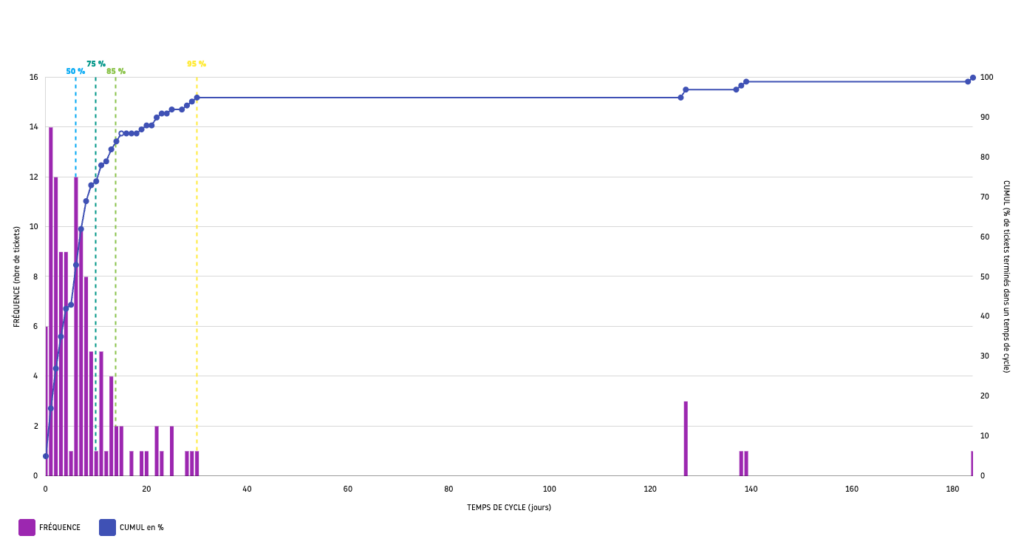
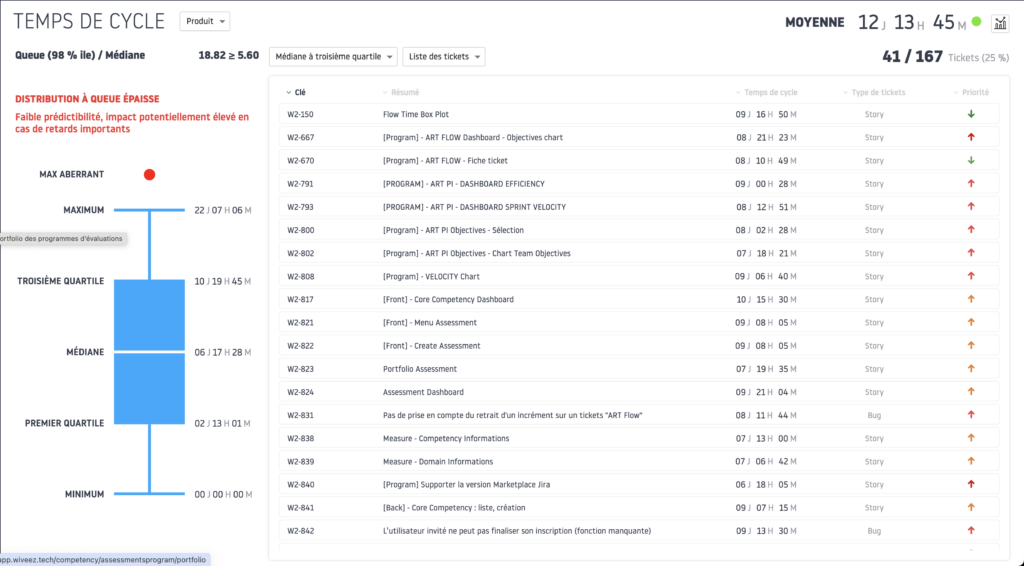
Exemple d’utilisation des Quartiles sur Wiveez

Suivi de la distribution des Temps de Cycle via les Quartiles
Histogramme de suivi du Temps de Cycle – Les Quartiles permettent de mesurer la qualité de la répartition
Analyse de la répartition du Temps de Cycle et identification des valeurs aberrantes

UCL/LCL : Garder votre Processus sous Contrôle

Les limites de contrôle (UCL et LCL) sont des seuils statistiques utilisés dans les cartes de contrôle. Ils permettent de surveiller un processus pour détecter des anomalies et déterminer si celui-ci est stable.

  • UCL (Upper Control Limit) : Limite supérieure de contrôle.
  • LCL (Lower Control Limit) : Limite inférieure de contrôle. Ces limites sont généralement fixées à 3 écarts-types au-dessus et en dessous de la moyenne, ce qui signifie que 99,73 % des données devraient se situer dans cette plage dans un processus « sous contrôle ».

Utilité

Les limites de contrôle sont idéales pour détecter des anomalies dans un processus. Si une donnée tombe en dehors de ces limites, cela peut indiquer un problème qui nécessite une investigation (comme un changement inattendu de la performance).

UCL/LCL : Comment les calculer ?

Les limites de contrôle (UCL/LCL) sont utilisées dans les cartes de contrôle pour surveiller un processus. Elles sont basées sur la moyenne et l’écart-type, et définissent une plage de variation normale. Elles sont calculées en appliquant la règle des 3-sigma, soit trois écarts-types au-dessus et en dessous de la moyenne.

UNPL/LNPL : Comprendre la Variabilité Naturelle

Contrairement aux UCL et LCL, les limites naturelles du processus (UNPL et LNPL) ne sont pas basées uniquement sur des calculs statistiques, mais plutôt sur une compréhension approfondie du processus et des tolérances acceptées.

  • UNPL (Upper Natural Process Limit) : Limite supérieure naturelle.
  • LNPL (Lower Natural Process Limit) : Limite inférieure naturelle. Ces limites reflètent la plage de variation naturelle du processus, définie par des spécifications ou des tolérances acceptées, et non par des écarts statistiques seuls.

Utilité

Les limites naturelles sont particulièrement utiles lorsque vous avez une bonne compréhension empirique du processus ou lorsque des tolérances spécifiques doivent être respectées (par exemple, des normes industrielles ou des exigences client). Elles permettent d’éviter de sur-réagir aux petites variations tout en garantissant que le processus fonctionne dans la plage définie comme acceptable.

Exemple d’application

1 – Collecte des données et analyse de la distribution

  • En général, la première étape est d’identifier si le processus suit une distribution normale ou non. Les limites naturelles peuvent parfois être calculées de manière différente selon la distribution des données.

2 – Déterminer les tolérances acceptables (ou les spécifications)

  • Les UNPL/LNPL peuvent être basées sur des tolérances acceptées ou spécifications de performance définies par des besoins métiers, des exigences clients ou des standards internes. Si ces tolérances existent (par exemple, une équipe s’attend à livrer entre 15 et 25 tickets par itération), elles peuvent guider directement les calculs.
  • Si des spécifications ou des tolérances sont déjà établies, les limites naturelles peuvent être fixées en conséquence. Par exemple, si l’équipe considère qu’en livrant moins de 16 tickets ou plus de 26, elle sort de son comportement normal, alors :
    • LNPL = 16
    • UNPL = 26

3 – Calculer les limites naturelles basées sur la variabilité observée

  • Si vous n’avez pas de tolérances pré-établies, vous pouvez calculer les UNPL/LNPL en fonction des données historiques du processus.

3.1 – Calculer la médiane ou une moyenne ajustée

  • La médiane est souvent utilisée à la place de la moyenne si le processus a des valeurs aberrantes ou des variations asymétriques. Cela donne une mesure centrale moins influencée par des valeurs extrêmes.
  • Dans notre cas, la médiane des tickets livrés sur 10 périodes est :
    • Médiane = 20
    • Si vous utilisez la moyenne, celle-ci est : Moyenne(xˉ) = 20,3

3.2 – Calculer la plage naturelle de variabilité

  • La variabilité naturelle du processus est souvent estimée à partir de l’écart interquartile (IQR), qui mesure la dispersion entre les 25 % des données les plus basses et les 25 % les plus hautes.
  • Pour notre exemple, les quartiles sont les suivants :
    • Q1 (1er quartile)=19 : 25 % des tickets livrés sont inférieurs ou égaux à 19.
    • Q3(3e quartile)=22 : 75 % des tickets livrés sont inférieurs ou égaux à 22.
  • L’écart interquartile (IQR) est : IQR = Q3−Q1 = 22−19 = 3

3.3 – Calculer les limites naturelles

Une méthode courante consiste à multiplier l’IQR par un facteur, souvent 1.5×IQR, pour identifier la plage de variation acceptable.

Ainsi, les limites naturelles peuvent être calculées comme suit :

  • UNPL = Q3+1,5×IQR = 22+1,5×3 =22+4,5 = 26,5
  • LNPL= Q1−1,5×IQR = 19−1,5×3 = 19−4,5 = 14,5

3.4 – Ajuster les limites en fonction des observations et des spécifications

  • Une fois les limites initiales calculées, vous pouvez les ajuster en fonction des observations empiriques ou des objectifs du processus.
  • Par exemple, si votre équipe constate que livrer moins de 16 tickets ou plus de 26 tickets est inacceptable, vous pourriez fixer les UNPL/LNPL respectivement à ces valeurs, même si les calculs indiquent une légère variation.

Vous voyez, sur la base de cet exemple, que le UNPL et le LNPL est très complémentaire de la mesure avec les Quartiles en intégrant les limites à ne pas dépasser pour rester dans un système stable.

Comparaison des calculs UNPL/LNPL avec UCL/LCL

En reprenant notre exemple avec les tickets livrés :

  • Calcul des UCL/LCL (basé sur 3-sigma) :
    • UCL = xˉ+3σ = 20,3+3×2,33 = 27,29
    • LCL = xˉ−3σ = 20,3−3×2,33 = 13,31
  • Calcul des UNPL/LNPL (basé sur 1,5 x IQR) :
    • UNPL = 26,5
    • LNPL = 14,5

Les limites naturelles (UNPL/LNPL) sont donc un peu plus serrées que les limites de contrôle UCL/LCL, dans cet exemple.

Cela montre que les UNPL/LNPL reflètent davantage la variation naturelle du processus (basée sur les quartiles) que les limites de contrôle, qui se basent uniquement sur la moyenne et l’écart-type.

UNPL et LNPL sont calculés en se basant sur la variabilité naturelle et la compréhension empirique du processus, souvent avec des mesures comme les quartiles ou l’IQR.

Contrairement aux UCL et LCL, les limites naturelles ne visent pas uniquement à détecter des anomalies statistiques, mais à définir les limites de performance attendue d’un processus en fonction de sa capacité naturelle ou de spécifications externes.

Quand Utiliser les Quartiles, UCL/LCL, et UNPL/LNPL ?

La compréhension des quartiles, des limites de contrôle (UCL/LCL) et des limites naturelles (UNPL/LNPL) est essentielle pour une gestion efficace des processus. Voici comment et quand les utiliser :

  • Les Quartiles : Utilisez-les pour obtenir une vue d’ensemble de la répartition des données et identifier les tendances générales dans la performance du processus. Ils sont particulièrement utiles pour des analyses statistiques descriptives.
  • UCL/LCL : Utilisez les limites de contrôle lorsque vous souhaitez surveiller la stabilité statistique de votre processus et détecter des anomalies qui nécessitent une intervention immédiate.
  • UNPL/LNPL : Utilisez les limites naturelles lorsque vous avez besoin de fixer des tolérances spécifiques (basées sur des normes ou des exigences) et que vous voulez capturer la variabilité naturelle d’un processus sans réagir de manière excessive aux petites variations.

Conclusion

Comprendre la différence entre les quartiles, les UCL/LCL et les UNPL/LNPL est essentiel pour bien gérer la performance des processus.

Chacune de ces méthodes apporte une perspective différente, allant de la répartition des données à la surveillance statistique, en passant par la gestion des tolérances naturelles.

En apprenant à bien utiliser ces outils, vous pouvez améliorer la stabilité de vos processus, éviter les fausses alertes et maximiser l’efficacité.

Que vous cherchiez à surveiller la performance d’une équipe projet ou à optimiser un processus manufacturier, ces concepts vous aideront à prendre de meilleures décisions pour garder vos processus sous contrôle.