
Maîtriser la dynamique des flux de valeur – Un voyage à travers le Flow Time Histogram
Dans le paysage économique moderne, où la concurrence est féroce et les attentes des clients toujours plus élevées, la capacité d’une entreprise à maîtriser ses flux de valeur et à tenir ses engagements devient un facteur crucial de succès.
Le respect des délais de livraison, la qualité du produit, et la réactivité aux demandes du marché sont plus que jamais des pierres angulaires de la performance d’une entreprise.
Cependant, dans cet environnement dynamique, les perturbations sont inévitables, qu’elles soient internes ou externes.
La clé réside dans la capacité à anticiper, à comprendre et à gérer ces perturbations efficacement.
C’est là qu’interviens le Flow Time Histogram (Histogramme de temps de flux), un outil analytique puissant qui offre une vision claire et objective de la performance des processus de livraison.
Cet article vous emmène dans un voyage exploratoire à la découverte de cet instrument analytique fascinant.
Sans se limiter à de simples mesures, nous plongerons dans les profondeurs de ses capacités à révéler la dispersion temporelle des demandes dans un flux de valeur.
En nous appuyant sur les principes des quartiles et du célèbre modèle des « boites à moustaches » ou « Box Plot », nous dévoilerons comment cet histogramme peut non seulement éclairer le cycle de vie normal des demandes, mais aussi mettre en lumière celles qui perturbent le flux.
Le Flow Time Histogram – Fonctionnement
Le Flow Time Histogram est un outil d’analyse visuelle qui représente la distribution du temps nécessaire pour achever différentes tâches ou demandes dans un processus.
Cette représentation graphique permet aux équipes et aux organisations d’observer et d’évaluer la performance de leur processus de travail en termes de rapidité et d’efficacité.
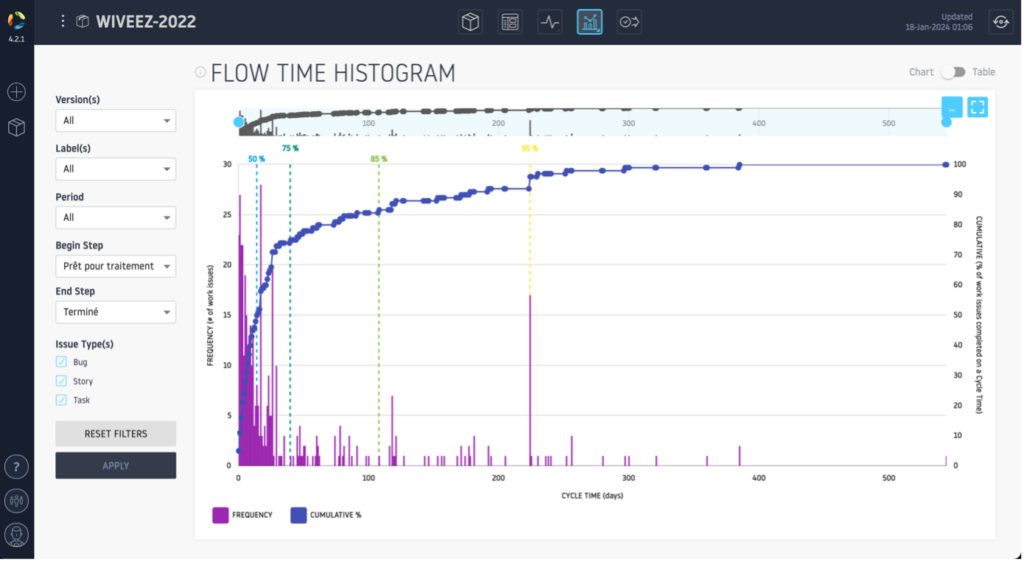
Collecte de Données : L’histogramme est construit à partir des demandes réalisées sur la période d’historique à analyser.
Axe Horizontal (X) : L’axe horizontal du graphique représente le temps. Il est divisé en intervalles (par exemple, jours, semaines) qui illustrent combien de temps chaque demande a pris pour être complétée.
Axe Vertical (Y) : L’axe vertical indique le nombre de demandes. Pour chaque intervalle de temps sur l’axe horizontal, il montre combien de demande a été achevée dans ce laps de temps.
Barres du Graphique : Chaque barre sur représente le nombre de demandes complétées dans un intervalle de temps spécifique. Par exemple, une barre pourrait montrer que 15 demandes ont été achevées en deux jours.
Le Flow Time Histogram – Comment l’analyser
Dispersion des Tâches : En examinant la distribution des barres, on peut observer la variabilité et la dispersion dans le temps de traitement des tâches.
Identification des Tendances : Des barres plus hautes dans certaines zones peuvent indiquer une concentration de tâches achevées dans un temps spécifique, révélant des tendances ou des modèles.
Analyse des Extremes : Les barres aux extrémités peuvent indiquer des anomalies, comme des tâches qui ont pris anormalement longtemps ou très peu de temps pour être complétées.
Utilisation des Quartiles : En intégrant l’analyse des quartiles, comme dans un box plot, on peut déterminer des mesures de tendance centrale (comme la médiane) et d’étalement, offrant une compréhension plus profonde du « temps de cycle » typique et des exceptions.
Le Flow Time Histogram est donc un outil précieux pour visualiser et analyser la performance du processus de travail. Il aide à identifier les goulots d’étranglement, à comprendre la variabilité dans les temps de traitement, et à prendre des décisions éclairées pour améliorer la fluidité et l’efficacité des flux de travail.
Le Flow Time Histogram – Analyser la répartition avec les Quartiles
La moyenne du Temps de Flux, bien qu’étant un élément intéressant de mesure de la performance du système, ne permet pas d’avoir une vision claire de la santé d’une chaîne de valeur et de la capacité de celle-ci à être prédictible.
Pour cela nous utiliserons plutôt la méthode des Quartiles.
Les quartiles sont des valeurs qui divisent un jeu de données en quatre parties égales, chacune contenant un quart (25%) des données. Ils sont essentiels dans la compréhension de la répartition et de la dispersion des données au sein d’un ensemble.
Voici une explication de chacun des quartiles et comment ils sont utilisés dans un box plot (boîte à moustaches) :
- Premier Quartile (Q1) : Aussi connu sous le nom de 25e percentile, le premier quartile divise les 25% des données les plus basses du reste. En d’autres termes, 25% des données sont inférieures ou égales à Q1.
- Deuxième Quartile (Q2) : Correspondant au 50e percentile, ce quartile est également connu sous le nom de médiane. Il divise l’ensemble de données en deux parties égales, avec 50% des données inférieures ou égales à Q2 et 50% supérieures ou égales.
- Troisième Quartile (Q3) : Le 75e percentile, ou troisième quartile, sépare les 75% des données les plus basses du quart supérieur des données. Autrement dit, 75% des données sont inférieures ou égales à Q3.
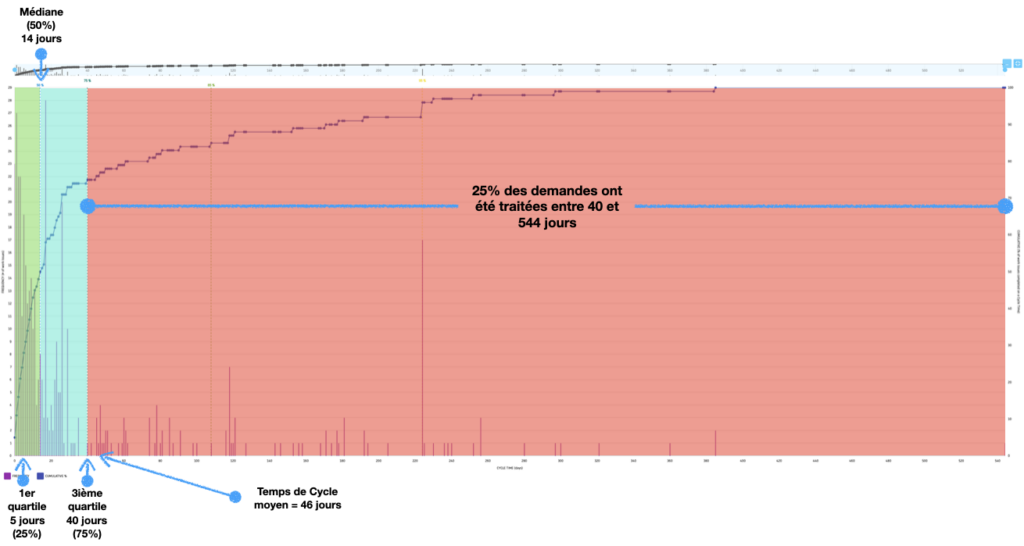
Le Flow Time Histogram, présenté ci-dessous, permet de mettre en évidence que 50% des tickets ont été réalisés en 14 jours ou moins, pour une moyenne de 40 jours sur l’ensemble des demandes. 25% des demandes ont été réalisées entre 40 jours et 544 jours, ce qui démontre une dispersion importante du flux de valeur, rendant la chaîne de création de valeur peu prédictible.
Le Flow Time Histogram – Identifier les valeurs Aberrantes avec le Box Plot (Boite à Moustaches)
Les valeurs aberrantes, dans le contexte d’un box plot (boîte à moustaches), sont des points de données qui se trouvent à une distance significative de la majorité des autres points dans l’ensemble de données. Elles sont considérées comme exceptionnelles soit parce qu’elles sont beaucoup plus grandes, soit beaucoup plus petites que la majorité des autres valeurs de l’ensemble de données.
Sur un box plot, les valeurs aberrantes sont généralement identifiées en utilisant l’écart interquartile (IQR), qui est la différence entre le troisième quartile (Q3) et le premier quartile (Q1). Les valeurs aberrantes sont celles qui se situent en dehors de la plage définie par 1,5 fois l’IQR au-dessus du troisième quartile ou en dessous du premier quartile. En d’autres termes, une valeur aberrante est un point de données qui est soit supérieur à Q3 + 1,5*IQR, soit inférieur à Q1 – 1,5*IQR.
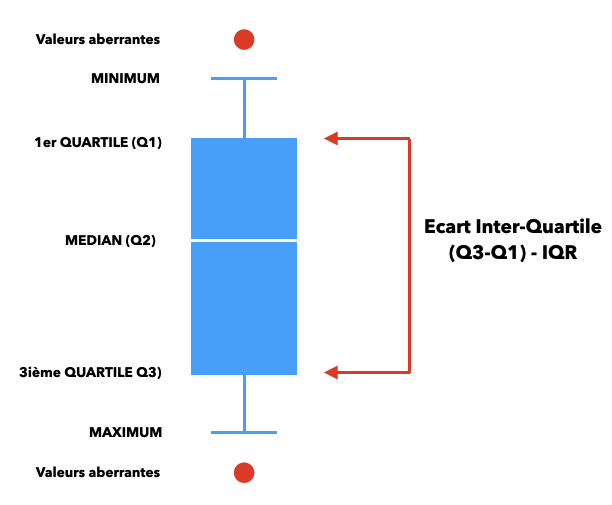
Un box plot utilise les quartiles pour fournir une représentation visuelle de la distribution, de la centralité et de la dispersion des données.
Boîte Centrale : La boîte centrale du graphique s’étend de Q1 à Q3, englobant donc la moitié médiane des données. La ligne à l’intérieur de la boîte représente la médiane (Q2).
Écart Interquartile (IQR) : Il s’agit de la différence entre le troisième quartile (Q3) et le premier quartile (Q1). L’IQR est une mesure de la dispersion des données et aide à définir les « moustaches » dans un box plot.
Moustaches : Les « moustaches » s’étendent depuis les bords de la boîte (Q1 et Q3) jusqu’aux valeurs minimales et maximales, dans une certaine limite, souvent définie comme 1,5 fois l’IQR au-delà des quartiles. Les données situées au-delà de cette limite sont souvent considérées comme des valeurs aberrantes et sont parfois représentées par des points distincts.
Appliquons le principe du Box Plot à notre Flow Time Histogram :
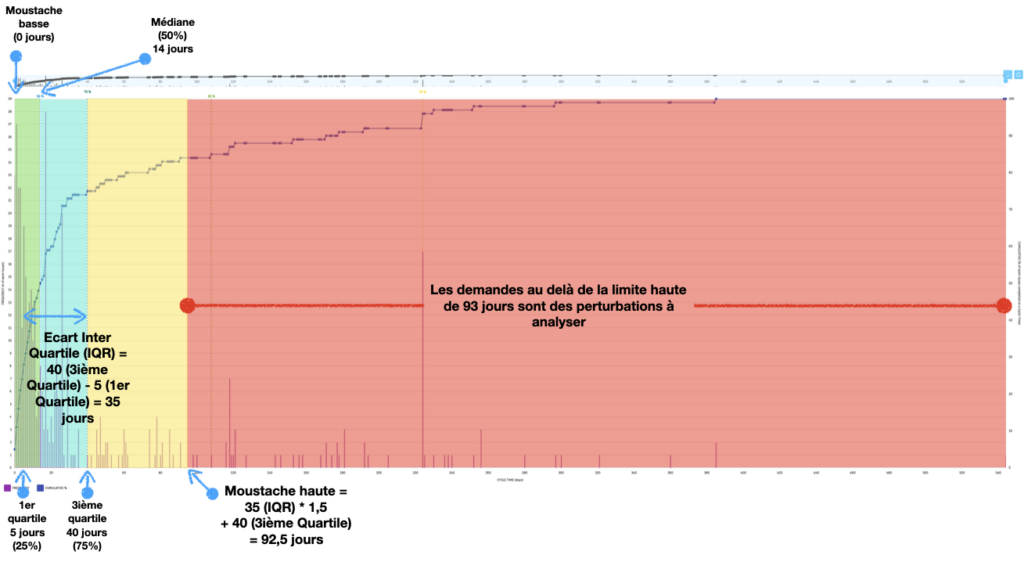
Le Premier Quartile (Q1) est de 5 jours et représente 25% des demandes
Le Second Quartile (Q2) est de 14 jours et représente la médiane, c’est-à-dire 50% des demandes traitées.
Le Troisième Quartile (Q3) est de 40 jours et représente 75% des demandes.
L’intervalle Inter-Quartile (IQR) correspond à la différence entre Q3 et Q1, soit 40-5 = 35 jours.
La moustache basse représente Q1-(1,5*IQR), soit 5 – (1,5*35). La valeur étant inférieure à 0, la moustache basse prend la valeur Zéro.
La moustache haute correspond à Q3 + (1,5*IQR), soit 40 + (1,5*35) = 92,5 jours, arrondi à 93 jours.
Conclusion : Toutes les demandes ayant mises plus de 93 jours à être traitées peuvent être considérées comme des valeurs aberrantes.
Il est important de noter que les valeurs aberrantes ne sont pas nécessairement des erreurs ou des données incorrectes ; elles peuvent indiquer une variabilité réelle dans les données ou mettre en évidence des phénomènes spéciaux ou des exceptions à examiner plus en détail.
L’identification et l’analyse des valeurs aberrantes sont cruciales pour une analyse de données approfondie, car elles peuvent avoir un impact significatif sur les conclusions tirées des données.
Le Flow Time Histogram – Analyser la qualité de votre distribution
En complément de l’analyse des Quartiles et des valeurs aberrantes, vous pouvez également étudier la qualité de la distribution du flux de valeur grâce à la théorie des probabilités, afin de savoir si votre courbe de flux est une « Fat-Tailed » ou une « Thin-Tailed ».
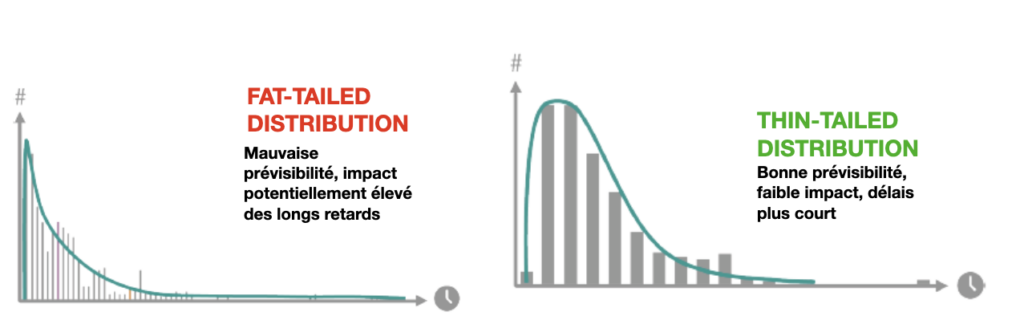
Les termes « Fat-Tailed » (à queue épaisse) et « Thin-Tailed » (à queue fine) sont utilisés pour décrire la forme des queues d’une distribution de probabilité dans le contexte des statistiques et de la théorie des probabilités.
Fat-Tailed (à queue épaisse): Une distribution est dite « Fat-Tailed » lorsque ses queues (les extrémités de la distribution) sont plus épaisses et plus lourdes par rapport à une distribution normale (gaussienne). Cela signifie que la probabilité d’observer des valeurs extrêmes (très grandes ou très petites) est plus élevée que dans une distribution normale.
Les distributions Fat-Tailed ont des kurtosis (caractérise le pic relatif d’une distribution par rapport à la distribution normale) élevés, ce qui indique une concentration plus importante de valeurs dans les queues. Ces distributions sont particulièrement importantes dans les domaines comme la finance, les sciences de la terre, et la gestion des risques, car elles peuvent mieux modéliser la probabilité d’événements rares mais extrêmes, comme les krachs boursiers ou les catastrophes naturelles.
Thin-Tailed (à queue fine): À l’opposé, une distribution est considérée comme « Thin-Tailed » lorsque ses queues sont plus fines et moins lourdes par rapport à une distribution normale. Les valeurs extrêmes sont moins probables dans une distribution Thin-Tailed que dans une distribution normale. Ces distributions ont des kurtosis inférieurs et sont moins susceptibles de produire des valeurs aberrantes extrêmes. Elles sont souvent utilisées pour modéliser des phénomènes où les événements extrêmes sont très improbables ou moins significatifs pour l’analyse.
Pour identifier la dispersion nous allons utiliser deux valeurs importantes : Le 98e percentile et la médiane. Le 98e percentile représente la valeur en dessous de laquelle 98% des données se trouvent. Autrement dit, seuls 2% des points de données sont supérieurs à cette valeur.
Le rapport entre le 98e percentile et la médiane permet d’évaluer à quel point les valeurs extrêmes sont éloignées de la valeur centrale de l’ensemble des données.
Un rapport élevé indique que les valeurs extrêmes (dans la queue de la distribution) sont significativement plus grandes que la majorité des autres valeurs, ce qui est caractéristique des distributions à queue épaisse.
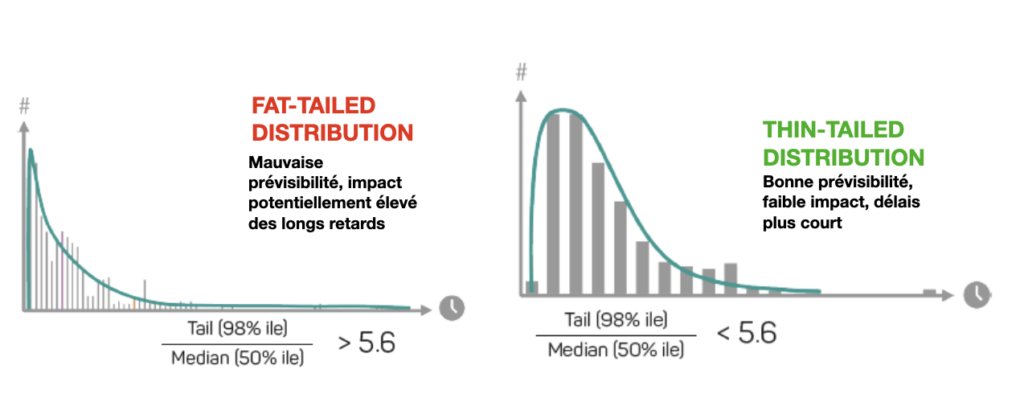
- Si le rapport 98e / Médiane est supérieur à 5.6, cela indique que la distribution a des queues relativement épaisses (FAT-TAILED), signifiant que les valeurs extrêmes sont non seulement présentes mais aussi beaucoup plus éloignées de la médiane. Cela peut être le signe d’une distribution avec une forte probabilité d’événements extrêmes par rapport à une distribution normale (gaussienne).
- Un rapport 98e / Médiane inférieur à 5.6 suggérerait une distribution moins prononcée dans les extrêmes (THIN-TAILED), pouvant indiquer une distribution plus proche de la normale ou avec des queues moins épaisses.
Repartons de notre Flow Time Histogram, afin d’analyser le type de distribution.
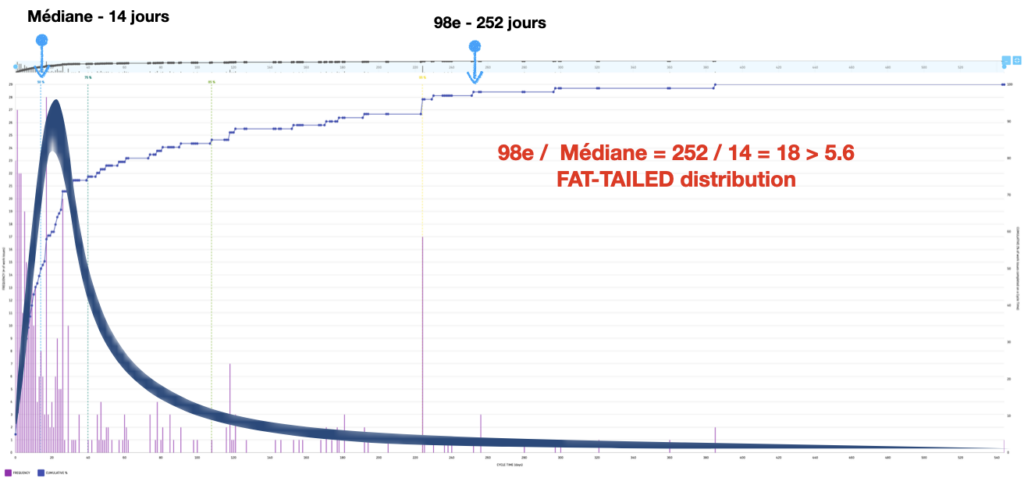
La médiane étant à 14 jours et la 98e percentile à 252 jours, nous obtenons un résultat de 18, largement supérieur à 5.6, ce qui représente une distribution lourde du flux le rendant non prédictible.
L’équipe en charge e la gestion de la demande et de la chaîne de valeur va devoir analyser les raisons de cette dispersion et mettre en œuvre les actions correctives afin de rendre le système plus prédictible et stable.
Conclusion
Dans le paysage économique actuel, où la concurrence est féroce et les attentes des clients sont toujours plus élevées, la capacité d’une entreprise à maîtriser ses flux de valeur et à tenir ses engagements devient un facteur crucial de succès.
Le respect des délais de livraison, la qualité du produit, et la réactivité aux demandes du marché sont plus que jamais des pierres angulaires de la performance d’une entreprise.
Cependant, dans cet environnement dynamique, les perturbations sont inévitables, qu’elles soient internes ou externes. La clé réside dans la capacité à anticiper, à comprendre et à gérer ces perturbations efficacement.
C’est ici qu’intervient le Flow Time Histogram, un outil analytique puissant qui offre une vision claire et objective de la performance des processus de livraison. À travers une visualisation graphique du temps nécessaire pour compléter chaque tâche, le Flow Time Histogram révèle non seulement la vélocité et l’efficacité des flux de travail, mais permet également d’identifier les anomalies et les variations qui peuvent perturber le cycle de livraison.
En mettant en lumière les tendances cachées et en quantifiant la variabilité du temps de traitement, cet outil aide les entreprises à diagnostiquer les causes profondes des retards et des inefficacités, leur permettant ainsi de prendre des mesures correctives ciblées.
L’adoption du Flow Time Histogram n’est pas simplement une question d’amélioration de processus ; il s’agit d’un engagement envers une culture de transparence et d’amélioration continue.
En offrant une vision claire de la performance du flux de valeur, cet outil permet aux entreprises de renforcer leur fiabilité, d’optimiser leur réactivité, et, finalement, de solidifier la confiance de leurs clients et partenaires.



